![[ Mælström ]](/neil.jpeg)
This data is for an array of records, each 68-bytes long, with a key defined by a comparator. The goal is to find a permutation to put them in order by the key; except qsort, which actually moves the records and is included for comparison. I noticed quick and smooth tend to do relatively better as the record size increases.
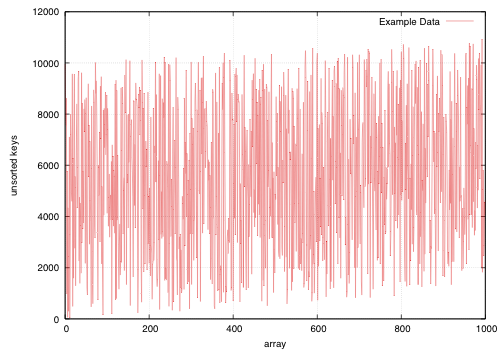
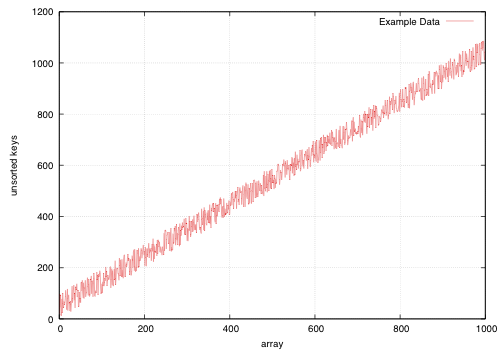
How the keys are arranged beforehand is given in the example sample data; each sample point is composed of 5 replicas using different seeds for the sample data.
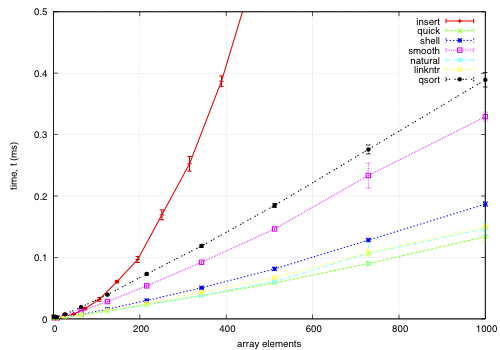
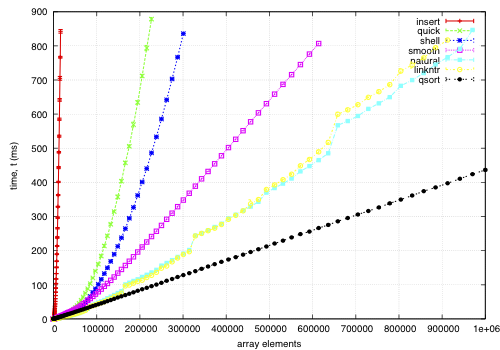
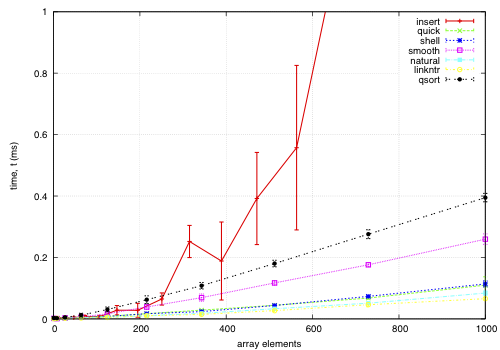
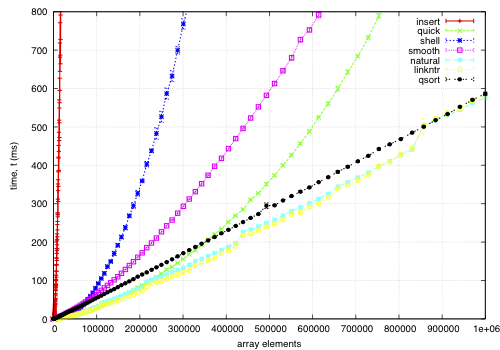
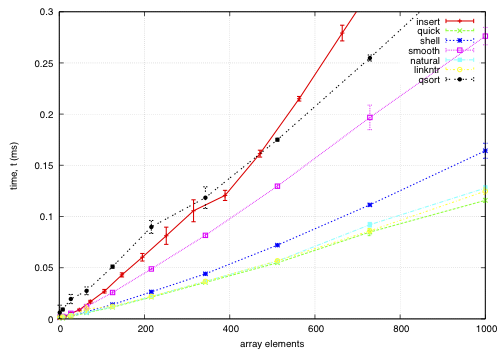
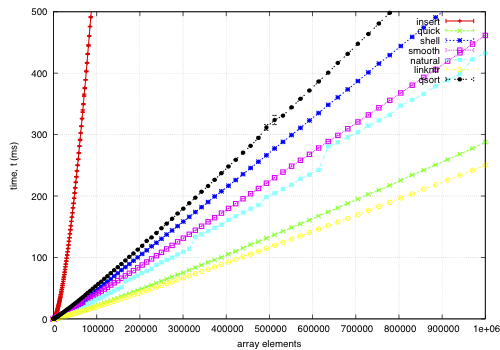
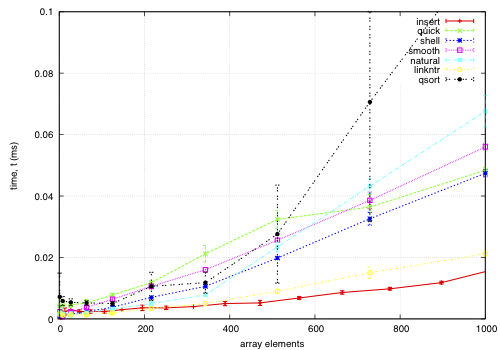
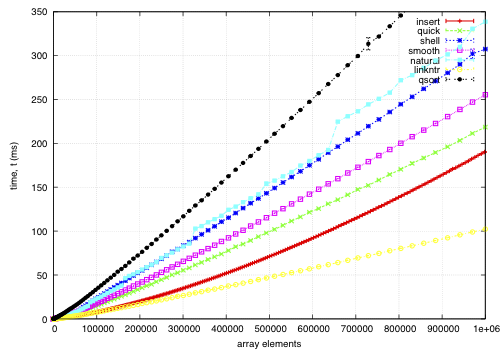
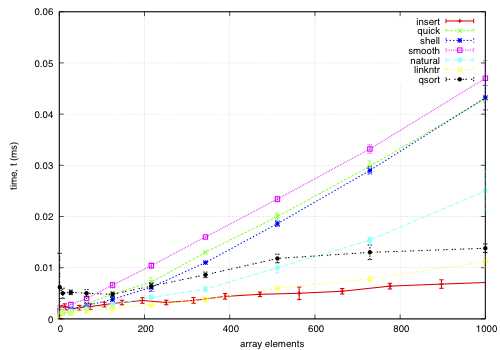
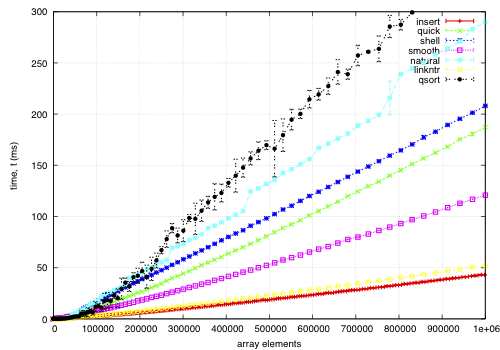
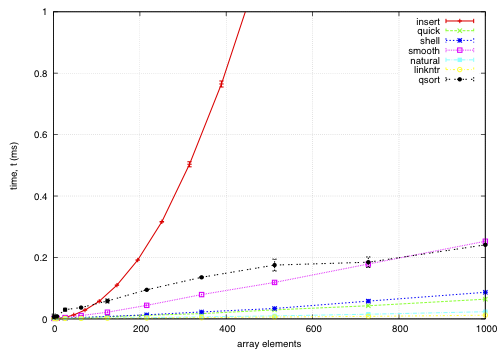
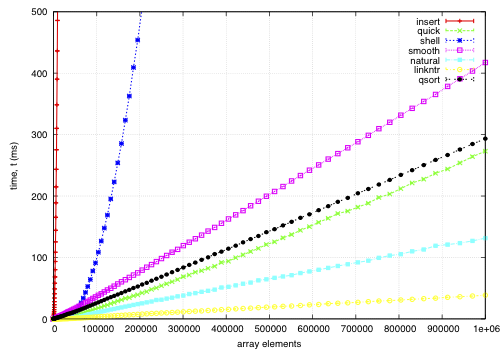
insert: O(nk) where k is the maximum distance an element is from it's sorted position. Stable, in-place, online, and super-adaptive. Very short to write. Works well when k is small, but is quadratic on randomised data.
quick: Quicksort is optimised per Bentley1993Engineering, Tukey1978Ninther. Despite the mainstream application of it everywhere, it's pretty good. It can degrade to O(n^2) in pathological cases; O(log n) stack space. Not adaptive, not stable, but great cache behaviour.
shell: Shell sort is just a couple of lines added to insertion sort; in most cases, Shell sort has enormous gains. Shell1959High's sequence gives O(n log^2 n) worst case; I used Ciura2001Best, an experimental improvement for the average run. It's still in place, but it's not stable, and it degrades to O(n log n) best case.
smooth: Dijkstra1981Smoothsort is magic; look at it's asymptotic running time. Smoothsort Demystified, Algorithm Implementation. It takes a lot of code, but it's awesome, if impractical.
natural: the space requirement of merge sort is O(n); that's problematic in general, but in this problem, we (at least can simulate) O(n) space with no extra cost by using the permutation as a scratch space. We want it to be adaptive, and if we add another O(n) space we could get it to be natural merge sort. If we greedily merge the sub-lists, then it becomes O(log n). The maximum size for a 32-bit addressing scheme is 124 bytes, and 64-bit is 504 bytes. It's naturally stable.
linkntr: this is greedy natural insertion-merge sort on linked-lists. When the two elements about to be merged are systematically of values different from each other, merge sort wastes a lot of time comparing elements with the first element. Peters2002Timsort (via McIlroy1993Optimistic) solves this by galloping, but we would like a simple solution that works without random access to the data. This takes natural, and, instead of merging right away, takes the larger list's inner element and inserts that into the smaller list; then it is merged from that point. If the merges are well balanced, (viz, insertion takes maximum time,) it should take twice as long on the merge step; however, we see that this has better performance overall. We tried having a threshold for merging, but the optimum value, in most cases, seems to be zero.
qsort: this uses the C library function qsort, and sorts the entire record instead of just the permutations on the index. qsort is fast in general; the bottleneck seems to be the size of the entire array, not the sorting itself. This cannot be meaningfully compared because it depends on the data size in a different way than the others'.
GitHub repository of the code.